在统计学的世界里,理解并掌握几个基本概念是通往深入探索统计分析原理与方法的钥匙,也是恰当选择统计分析方法、正确描述和解释统计结果的重要基石。以下,我们将对这些基本概念进行更为详尽的阐述。
一、同质与变异
同质(homogeneity):
同质,简而言之,即研究对象在某些特定方面或属性上具有相同或相似的状况。这种共性是统计分析的前提,它确保了我们可以将一组对象视为一个整体来进行研究。
在生物医学研究中,同质可能意味着研究对象在年龄、性别、种族、基础疾病状态等方面的相似性。这种相似性有助于我们更准确地揭示出特定因素与研究结果之间的关系。
变异(variation):
变异,则是指每个研究对象的变量值之间的差异。这种差异是生物医学数据最显著的特征之一,也是统计分析所要捕捉和解释的核心内容。
变异可能源于多种因素,如遗传因素、环境因素、测量误差等。在这些变异性的现象中,蕴藏着事物发展的必然规律和趋势。统计学的任务就是通过分析和对比这些变异,揭示出事物的本质特征和规律。
统计学的魅力在于,它能够从事物的同质性与变异性的数量表现出发,通过一定数量的对比和分析,像侦探一样揭示出隐藏在数据背后的秘密和规律。
二、抽样误差(sampling error)
定义:
抽样误差是由于抽样研究所致的样本指标与总体指标之间的差异。这种差异是不可避免的,因为样本只是总体的一部分,无法完全代表总体。
减少抽样误差的方法:
采用随机抽样方法:随机抽样能够确保每个研究对象都有相等的机会被选中,从而减小抽样误差。
增加样本量:样本量越大,样本指标越接近总体指标,抽样误差也就越小。
选择变异程度小的研究指标:变异程度小的指标意味着数据更加稳定,抽样误差也就相对较小。
三、假设检验(hypothesis test)
定义与原理:
假设检验,又称显著性检验,是应用统计学原理,由样本之间的差异去推断样本所代表的总体之间是否有差异的一种推断方法。
在抽样研究中,由于抽样误差的存在,当两个或多个样本均数(或率)有差异时,我们不能直接推断出总体之间也存在差异。这时,就需要进行假设检验来判断这种差异是仅由抽样误差所致,还是总体之间存在本质差异。
常用的假设检验方法:
t检验:用于比较两个样本均数之间的差异是否显著。
方差分析:用于比较三个或更多个样本均数之间的差异是否显著。
卡方检验:用于比较两个或多个总体率或构成比之间的差异是否显著。
秩和检验:用于比较两个或多个样本的中位数或分布位置之间的差异是否显著。
四、概率(probability)
定义与表示:
概率是描述随机事件发生可能性大小的一个变量,用p表示,其范围在0到1之间。
p值越接近0,表示事件发生的可能性越小;p值越接近1,表示事件发生的可能性越大。
小概率事件与统计意义:
通常将p≤0.05或p≤0.01称为小概率事件,表示该事件发生的可能性很小。在统计学中,我们将这种小概率事件看作事物差异有统计学意义的界限。
若p≤0.05或p≤0.01,我们可得出“差异有统计学意义”的结论;若p>0.05,则得出“差异无统计意义”的推论。
注意事项:
小概率事件不代表某事件绝对不可能发生。即使p值很小,仍有5%或1%犯错误的机会。因此,在下结论时不要绝对化,通常在研究中应报告p的精准值。
p值大小只能说明统计学意义上差异的“显著”程度,并不能完全说明临床意义上实际差异的“显著”程度。在解释统计结果时,应结合临床实际和专业知识进行综合判断。
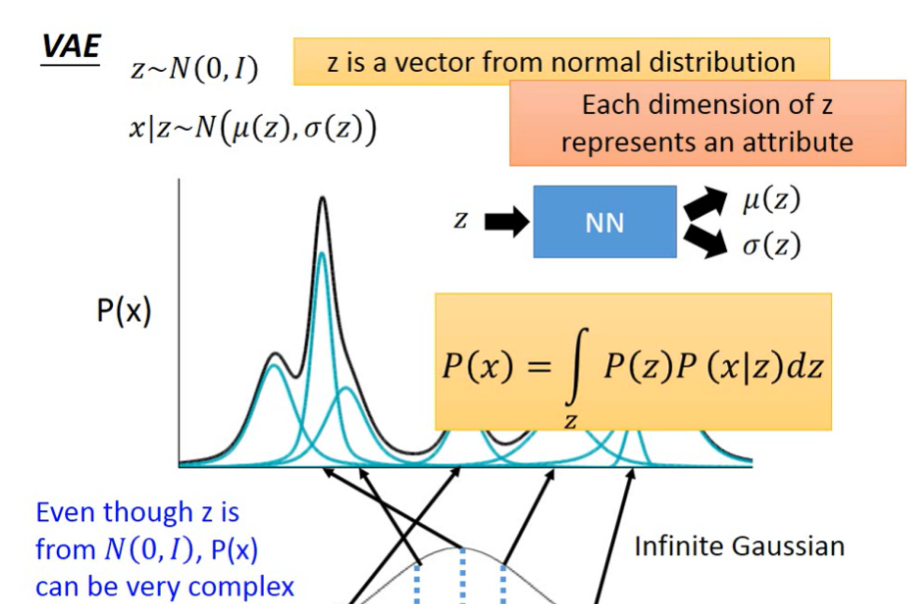
(图:概率分布或假设检验流程的图表)
综上所述,理解并掌握同质与变异、抽样误差、假设检验和概率等基本概念,是深入探索统计分析原理与方法、恰当选择统计分析方法、正确描述和解释统计结果的重要基础。在实际应用中,我们应结合具体研究情境和需求,灵活运用这些概念和方法,为科学研究和决策提供有力支持。